问:平面力系的平衡条件及其应用
1.物体的平衡状态
物体相对于地球处于静止状态和等速直线运动状态,力学上把这两种状态都称为平衡状态。
2.平衡条件
(1)二力的平衡条件:作用于同一物体上的两个力大小相等、方向相反、作用线相重合,这就是二力的平衡条件。
(2)平面汇交力系的平衡条件:一个物体上的作用力系,作用线都在同一平面内,且汇交于一点,这种力系称为平面汇交力系。平面汇交力系的平衡条件是∑X=0和∑Y=0。
(3)一般平面力系的平衡条件还要加上力矩的平衡,所以平面力系的平衡条件是∑X=0、∑Y=0和∑M=0。
3.利用平衡条件求未知力
一个物体,重量为W,通过两条绳索AC和BC吊着,计算AC、BC拉力的步骤为:首先取隔离体,作出隔离体受力图;然后再列平衡方程,∑X=0、∑Y=0,求未知力T1、
T2,如图1―2、图1―3所示

4.静定桁架的内力计算
(1)桁架的计算简图如图1-4所示。
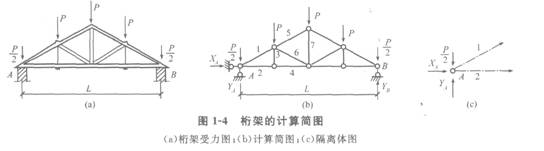
首先对桁架的受力图进行如下假设:
1)桁架的节点是铰接;
2)每个杆件的轴线是直线,并通过铰的中心;
3)荷载及支座反力都作用在节点上。
(2)用节点法计算桁架轴力:先用静力平衡方程式求支座反力XA、YA、YB,再截取节点A为隔离体作为平衡对象,利用∑X=0和∑Y=0求杆1和杆2的未知力。
(3)用截面法计算桁架轴力:截面法是求桁架杆件内力的另一种方法,如图1-5所示。

首先,求支座反力YA、YB、XA;然后在桁架中作一截面,截断三个杆件,出现三个未知力:N1、N2、N3。可利用∑X=0、∑Y=0和∑MG=0,求出N1、N2、N3。
5.用截面法计算单跨静定梁的内力
(1) 梁在荷载作用下的内力:图1-6为一简支梁。梁受弯后,上部受压,产生压缩变形;下部受拉,产生拉伸变形。V为1―1截面的剪力,∑Y=0,V=YA。1 ―1截面上有一拉力N和一压力N,形成一力偶M,此力偶称1―1截面的弯矩。根据∑M0=0,可求得M=YA?a。梁的截面上有两种内力,即弯矩M和剪力 V。
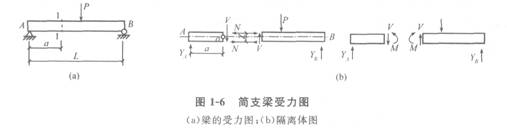
(2)剪力图和弯矩图如图1―7所示,找出悬臂梁上各截面的内力变化规律,可取距A点为χ的任意截面进行分析。首先取隔离体,根据∑Y=0,剪力V(χ)=P;∑M=0,弯矩M(χ)=-P?χ。不同荷载下,不同支座梁的剪力图和弯矩图,如图1―8和图1-9所示。
小编推荐:
点击这里查看一级建造师考试最新资讯
想要顺利通过一级建造师考试吗?点击立即做题:一级建造师考试题库